Unity provides standard spline asset,
use BGCurve only if Unity spline misses some feature
Math
Math methods
1
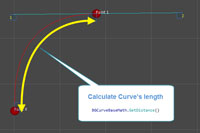
Spline's distance ( math.GetDistance() ). Example
2
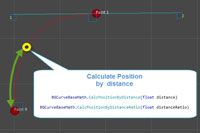
Position by distance ( math.CalcPositionByDistance(float distance) or math.CalcPositionByDistanceRatio(float distanceRatio) [Range (0,1)]). Example
3
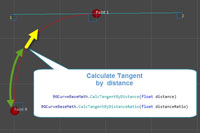
Tangent by distance ( (math.CalcTangentByDistance(float distance) and math.CalcTangentByDistanceRatio(float distanceRatio) [Range (0,1)]). Example
4
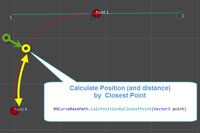
Position and distance(optionally) for a point, which is on the spline and closest to some other point, which can be anywhere (math.CalcPositionByClosestPoint(Vector3 point)). Example
Understanding Math
Math gives you access to some of the essential methods for dealing with splines.
Math always operate with world coordinates.
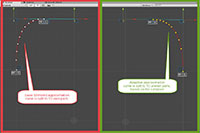
Math calculates it's data by splitting the spline to small straight lines. There are 2 types of approximations available with BGCurve:
1) Uniform (by splitting every spline section to even parts) and
2) Adaptive (also uniform, but points may be skipped based on spline's curvature and added then necessary). Adaptive split may result with much lesser points and better approximation (however it may be slower).
If spline changed, math recalculates it's state. Math is contained in separate classes (BGCurveBaseMath and BGCurveAdaptiveMath). If you were using math and do not need it anymore, you'd better call math.Dispose() method ASAP. If you need math, we recommend you to use BGCcMath component, which gives you easy access to math parameters and operations. Read about BGCcMath under components section.
1) Uniform (by splitting every spline section to even parts) and
2) Adaptive (also uniform, but points may be skipped based on spline's curvature and added then necessary). Adaptive split may result with much lesser points and better approximation (however it may be slower).
If spline changed, math recalculates it's state. Math is contained in separate classes (BGCurveBaseMath and BGCurveAdaptiveMath). If you were using math and do not need it anymore, you'd better call math.Dispose() method ASAP. If you need math, we recommend you to use BGCcMath component, which gives you easy access to math parameters and operations. Read about BGCcMath under components section.
Updating Math
By default if curve is changed math is recalculating its data once per frame.
It's done like this to minimize overhead for multiple changes.
If you need all the changes to be immediately reflected in math component, you can manually call math.Recalculate() method.